みなさま、こんにちは。開発部の川浦です。
CADでモデリングをする際に以下のようなお困りごとはないでしょうか?
- 立体的な形状パターンを多用したいが、複雑すぎてコントロールできない!
- 節点が多すぎてブーリアンが失敗する!
そんな悩みもnTopologyなら解決できるかもしれません。
今回はnTopologyの特徴であるインプリシットモデルについてご紹介いたします。
インプリシット(陰関数)モデルとは
現在の主要なCADソフトで採用されているのはB-rep(境界表現)モデルです。B-repの詳細な仕組みはここでは割愛しますが、多数の面(特に曲面)が交差する複雑な形状を作ろうとすると、処理に時間がかかったり失敗することがあります。
これに対してnTopologyはインプリシットモデルを採用しています。「インプリシット」は陰関数(Implicit Function)からきているのですが、これも要点だけ説明しますと、
- 方程式 F(x, y, z)=0 が成立する数式で形状を定義する(x, y, zは座標)
というコンセプトです。具体的な例と利点を見ていきたいと思います。
インプリシットモデルの例
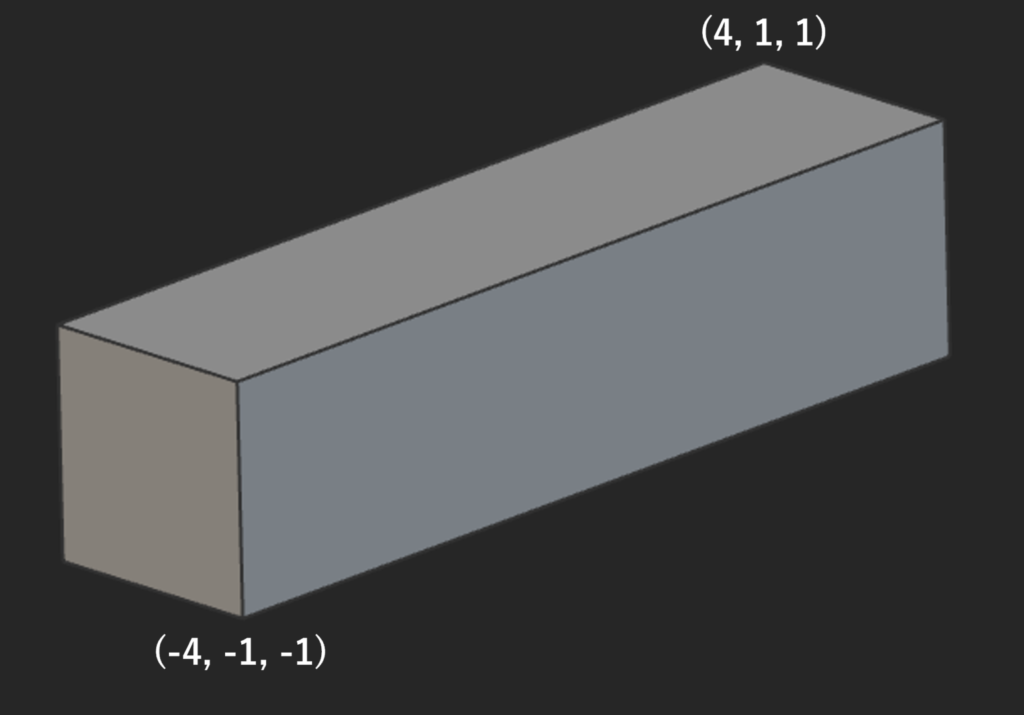
例えばCADで作成した上の図のような形状、人間の目から見ればごく普通の直方体ですが、ソフトウェアから見たデータとしてはどうでしょうか?
8つの頂点と12のエッジ、6つのフェイス、面は全て外側を向いて隙間なく閉じている、という情報まであって初めてソリッドモデルと認識されます。
同じ形状をインプリシットモデルで再現する場合、必要な情報は次の数式になります。
Fa(x, y, z) = max(|x|-4, |y|-1, |z|-1)
これだけです。
ここでFa=0が成立する座標(例えば4, 0.3, -0.8など)は全てこの直方体の表面部分に一致します。
また、Fa<0となる座標(例えば0, 0, 0など)は全て直方体の内側となります。
すなわち、Fa(x, y ,z)=0の陰関数表現を境界としてソリッドか否かを識別しているのがインプリシットモデリングです。
nTopologyでの実装方法
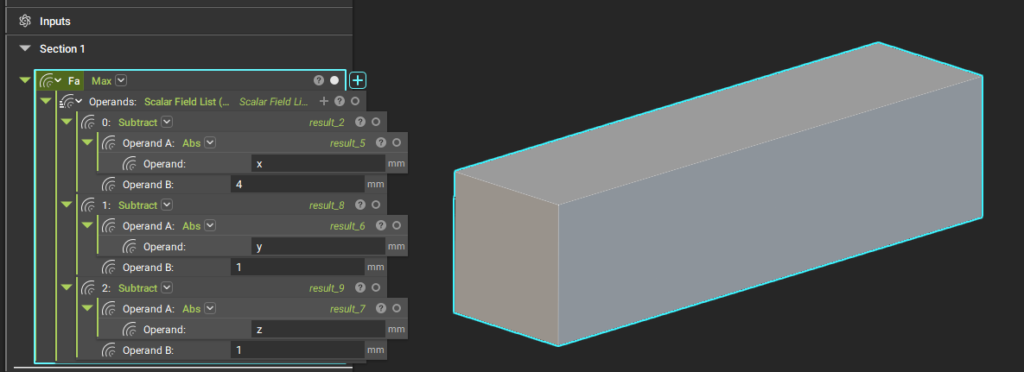
nTopologyでは数式ブロックの組み合わせで先の直方体を表現することもできます(下図左)が、あまりに直感的でないので通常は使用しません。
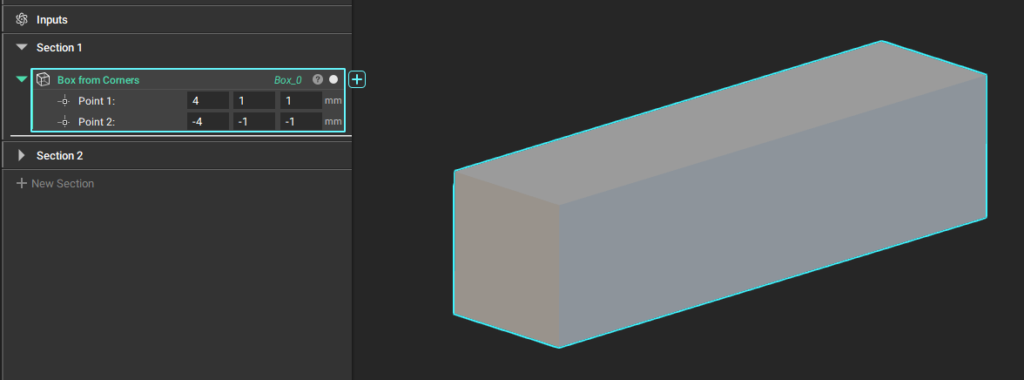
基本立体(プリミティブ立体)については予めブロックが用意されているのでそちらにパラメータを入力して使用します。(下図右)
実装方法は違えど表示するために内部で処理している数式は同じです。
逆にプリミティブとして用意されていない形状も、数式が分かっていれば自由に作成することが可能です。
インプリシットモデルのブーリアン演算
nTopologyの謳い文句に「ブーリアン演算が絶対に失敗しない」とあるのも、インプリシットモデルを採用しているのが理由です。
例としてもう一つ、数式でインプリシットモデルの球(R=2)を定義します。
Fb(x, y, z) = √(x^2+y^2+z^2)-2
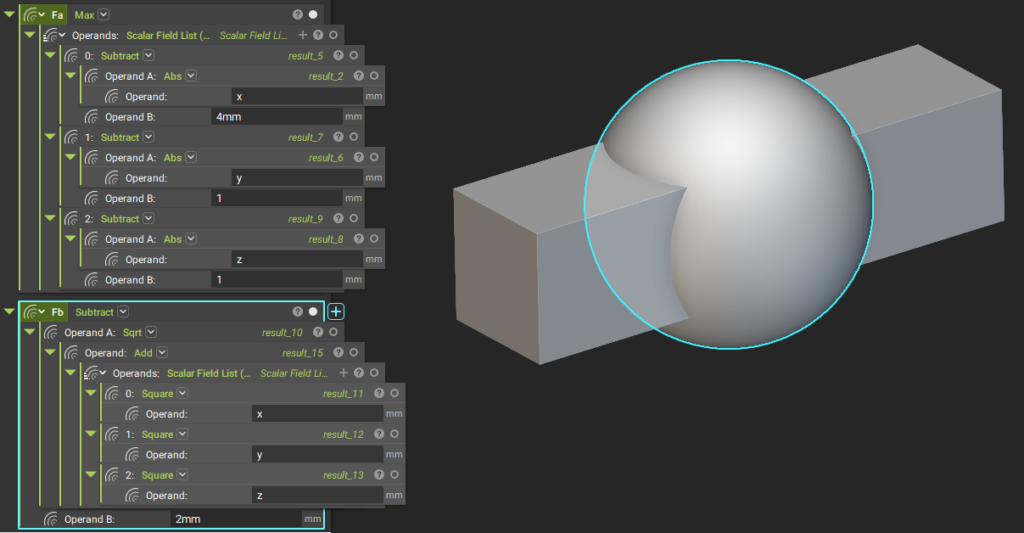
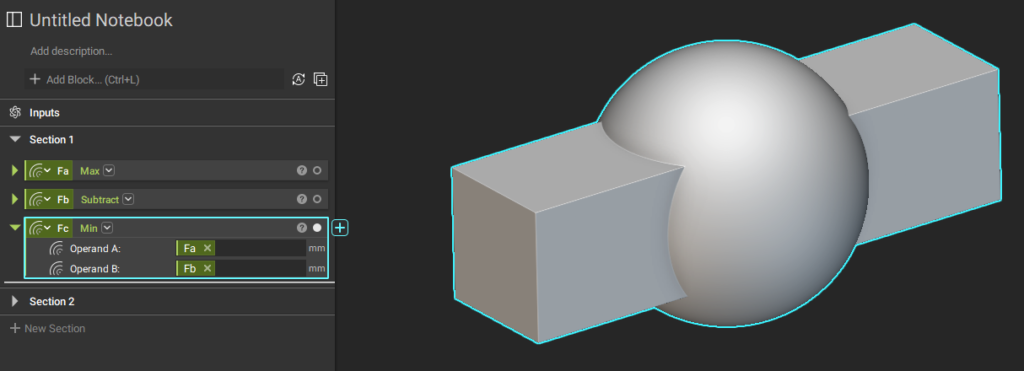
この球Fbと先ほどの直方体Faとのブーリアン演算の和Fcは
Fc(x, y, z) = min(Fa, Fb)
で定義されます。
これはFaとFbどちらか(もしくは両方)が負の値になる座標は、Fcでも負の値(=ソリッド部)になるという意味です。
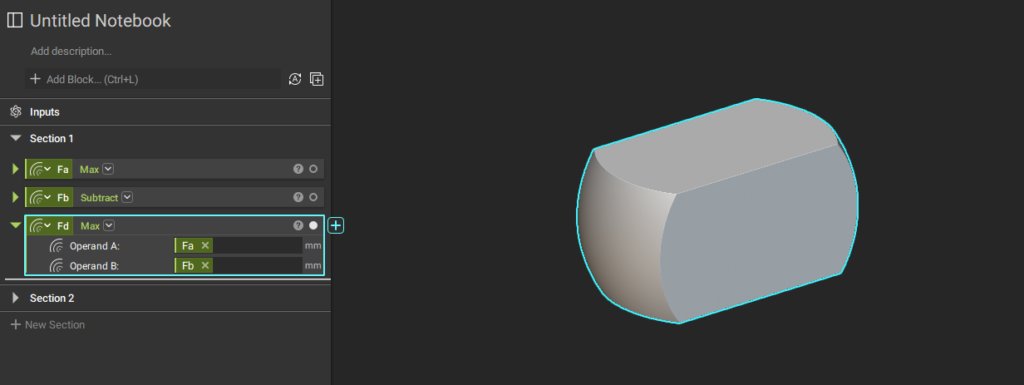
また、次の数式はブーリアン演算の積を表します。
Fd(x, y, z) = max(Fa, Fb)
これはFaとFbの両方が負の値になる座標だけ、Fdも負の値(=ソリッド部)になるということです。
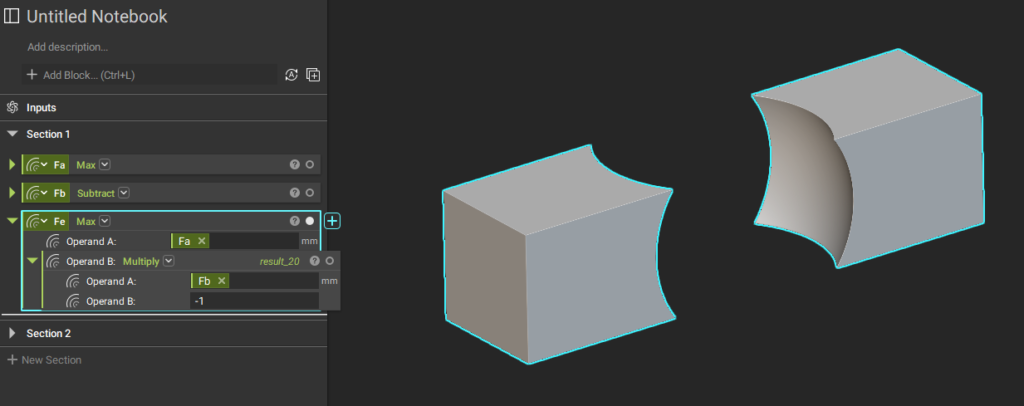
ここで片方の正負を逆にするとブーリアン演算の差ができます。
Fe(x, y, z) = max(Fa, -Fb)
通常のnTopologyの操作ではこういった数式を意識する必要はありません。(覚えておくと役に立つことはあります)
個別の形状を、対応するブーリアン演算のブロックに入れていくだけです。
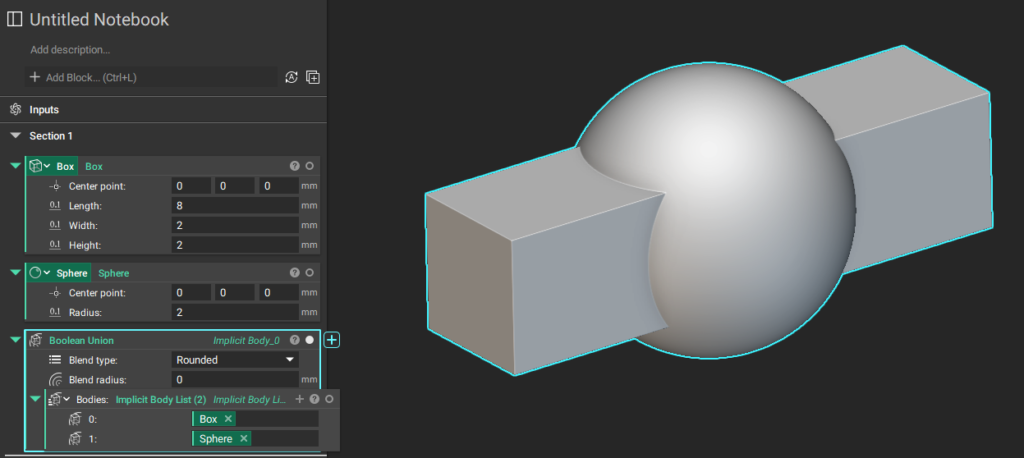
ここではシンプルな形状を例にしましたが、どんな複雑な形状であっても数式として表すことができればブーリアン演算はそれらの組み合わせの正負を見るだけで、交差するポイントやカーブの計算をする必要がありません。
インプリシットモデルであれば下図のようにTPMSとラティスが交差するような形状でも破綻することがないのです。

インプリシットモデルと距離フィールド
以前の記事でフィールドについてご紹介しましたが、距離フィールドは形状を定義している数式そのものです。
境界面の値はゼロで、内側は負の値に収束し外側は無限に大きくなっていきます。

逆に言いますと、単位が距離(mm)のフィールドに負の値が含まれていればそこはソリッドとして認識されます。
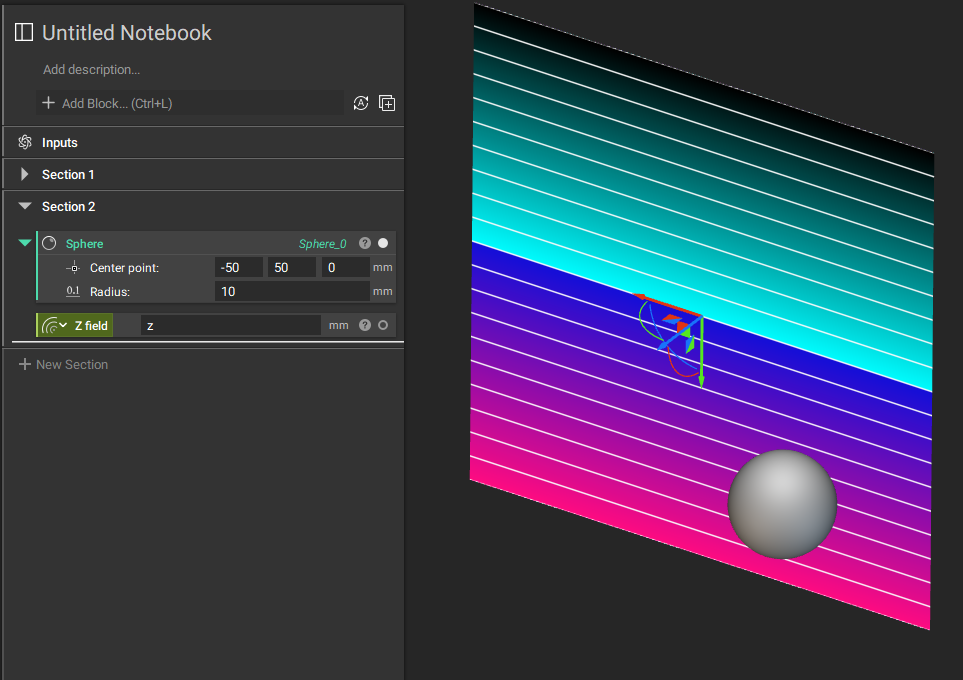
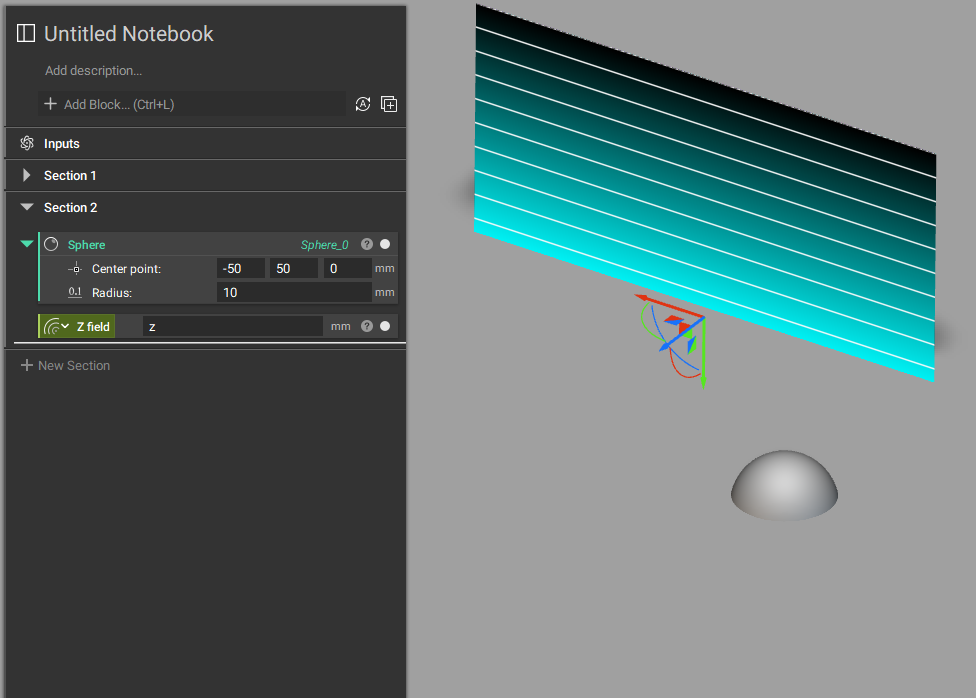
例えばZ座標の値だけを示すフィールドは、原点からマイナス方向がすべてソリッドと認識されるため、XY方向に無限の広さを持つ地面のように表示できます。(下図参照)
インプリシットモデルの注意点
インプリシットモデルは頂点やエッジ、フェイスの情報を持っていない為、それらを直接触ることは一切できません。
つまりCADソフトで当たり前にできるような、「2つの頂点を選択して距離を測る」といったことができません。
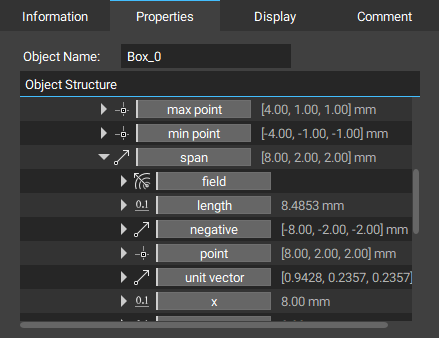
モデルのプロパティから最大座標やスパンベクトルなどを参照したり、それらを使用した計算ブロックを作成する必要があります。
インプリシットモデルの汎用性
複雑形状を作る上でメリットの多いインプリシットモデルですが、残念ながら現状ではnTopology以外で扱っているソフトはほとんどなく、3Dプリンタや工作機械にそのまま形状データを引き渡すことができません。
より一般的なスライスデータやメッシュモデル、CADなどの汎用形式に変換する必要があり、そういった機能もnTopologyは持ち合わせていますので、次回の記事ではインプリシットモデルとの相互変換と入出力についてご紹介したいと思います。
参考記事
Implicit modelling for complex geometry
いかがでしたでしょうか。
導入のご相談やデモのご希望など、nTopologyに関するご質問はお問い合わせまでお願いいたします。


